pH of any acid/base solution
What is pH of solution of a monoprotic acid? Let's try the general approach described in the general case section. Equilibrium in solution is described by the set of the following equations:
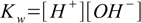 6.1
6.1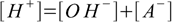 6.2
6.2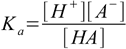 6.3
6.3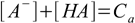 6.4
6.46.1 and 6.3 describe equilibrium, 6.2 is a charge balance - solution must be neutral, 6.4 is a mass balance and reflects the fact, that sum of concentrations of all acid forms present in the solution must be identical to the concentration of acid added.
Combining 6.1 and 6.2 we get
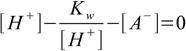 6.5
6.5From 6.4
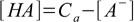 6.6
6.6Substituting 6.6 into 6.3 yields
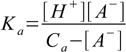 6.7
6.7We solve 6.7 for [A-] and substitute it into 6.5:
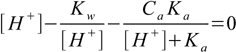 6.8
6.8Which - when expanded - gives third degree equation for [H+]:
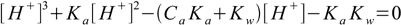 6.9
6.9This equation describes any solution of any monoprotic acid (just remember the concentration/activity thing described in the ionic strength and activities section). To calculate pH we need to know Ca and Ka and the final result will be correct regardless of their values - doesn't matter if acid is strong or weak, or if it is concentrated or diluted (neglecting activity calculations). This is the ultimate equation for pH calculation of monoprotic acid solution.
And what about bases? Using exactly the same method as above we can get equation for [OH-]:
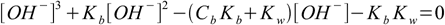 6.10
6.10which is almost identical with 6.9. We can also use conjugate Ka definition and solve directly for [H+]:
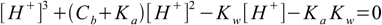 6.11
6.11See also pH calculation for salt section for more interesting information.
Equations in this form are unusable for hand calculations. There are two things that can be done. We can try to simplify the equations (see strong acid/base and weak acid/base sections), or we can use numerical method to find polynomial root - see Newton method section.

